こんにちは!ライターのporukaです。
突然ですが、あなたは確率と統計の違いを説明することはできますか?
お恥ずかしながら、塾講師をやっている私も参考書を見ずに説明しろと言われたら無理です。
ましてや数学が苦手な人にも理解できるようにとなると。
あなたも学校で習った時の用語を駆使すれば説明できるでしょうが、それを数学が苦手な人にそのまま言っても通じません。
なので、今回いい機会なので確率と統計の違いについて徹底的に勉強しようと思います。
まずは塾講師の私が理解して、それを分かりやすくあなたに解説しようと思います。
スポンサーリンク
目次
確率とは
確率とはどういう意味なのか小学生が使う国語辞典で調べてみました。
「あることが、どの程度のたしかさで起こるかというわりあい」
引用:小学館例解学習国語辞典第十版<ワイド版>
と書かれていました。
さすがに小学生が使う国語辞典だけあってかなり分かりやすい説明です。
でも、数学の苦手な人は割合と聞いただけで拒否反応を示す人もいます。
なので、具体例を出して解説しようと思います。
問題:さいころ1個をふって2の出る確率を求めよ。
まず、さいころには1~6の数字が一つずつ書いてありますよね。
ということは、さいころの出目のパターンは6つということになります。
そのうち、2が出る割合はというと、
1÷6=1/6
となります。
この式が成り立つためには条件があります。
それは、さいころには細工がされておらず、すべての目が同じたしかさで出るというものです。
スポンサーリンク
統計とは
確率の時と同じように国語辞典で統計の意味を調べました。
「多くの集まりの中での、あることがらの分布を数で表し、全体がよくわかるようにすること」
引用:小学館例解学習国語辞典第十版<ワイド版>
となっています。
これでも十分分かりやすいとは思いますが、具体例を挙げて解説していきます。
問題:10人で受けたAテスト、Bテストがある。その結果は次のようになった。
Aテストは平均点65点、Bテストは平均点72点
どちらのテストが受験者の習熟度が高いと言えるか?
単純に考えるなら答えはBテストになりますよね。
こちらのグラフをご覧ください。
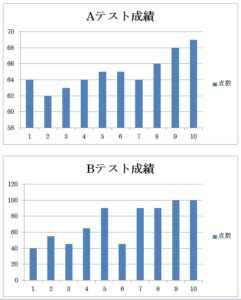
この二つのデータを見ると、Aの方はまんべんなくできていますが、Bの方は二極化しています。
出来る人は満点に近く、出来ない人は40点と低い点数です。
これから言えることは、Aの方は受験者の理解度はほぼ等しく、Bの方は平均点付近の人はおらず出来る人と出来ない人にはっきり別れているということです。
結局、問題の答えはというと、Aの方が受験者の習熟度が高いと言えます。
なぜかというと、Aの方の受験者はみんな理解度が等しいため極端に簡単でも難しくもないという感想をもつでしょう。
しかし、Bの方は受験者によって簡単、または物凄く難しいという感想をもちます。
よって、Aの方が受験者の習熟度は高いと言えます。
ちなみに、このデータは問題集のコピーではなく自作ですよ。
私は数学が得意な方なので。
ただ、このデータをエクセルでグラフにする作業に四苦八苦しました。
統計について分かりやすく説明してくれる動画を見つけたのでご覧ください。
【初心者のためのやさしい統計学講座】
私もこの動画を見て学習しました。
今の世の中色んなことを教えてくれる動画があるので独学がしやすいですよね。
いい時代になりましたね。
数学的確率と統計的確率の具体例

数学的確率と統計的確率の具体例について挙げていきます。
<数学的確率>
● コイン1枚を上に投げて着地したときに表になる確率
● 赤玉2個、白玉3個が入った袋の中から白玉を1個引く確率
<統計的確率>
● バッターが次の打席でヒットを打つ確率
● 明日の降水確率
以上の具体例から分かるように数学的確率は過去のデータを使わずに理論的に求めることが出来て、統計的確率は過去のデータを使い、次におこることを予測するものと言えるのではないでしょうか。
この違いをはっきりと理解している人は少ないのかもしれません。
私もその中の一人でしたし。
そもそも、数学的確率とか統計的確率なんて言葉自体知らなかったです。
人間って興味のないものには本当に疎い生き物ですよね。
まとめ
確率と統計の違いについておさらいすると、
● 確率はどの程度起こるかを理論的に計算して出せるもの
● 統計はいくつかのデータを収集して、その傾向や性質がどのように分布しているかをみるもの
● 数学的確率はみんながいうところの確率
● 統計的確率は過去のデータをもとに色んなことを予測する確率
出来うる限りで分かりやすく解説してきましたが、おわかりいだだけたでしょうか?
意識したことは数学用語を極力使わないようにすることです。
今回正直自分にとってもよく分からないテーマだったので色々調べて勉強しました。
なんでもそうですが、分かってくると楽しくなりますよね。
しかも、私の場合塾講師としての仕事につなげられるので大変意義のある記事を書くことができました。
仕事で統計が必要になる場面は多いですよね。
例えばある商品のよく売れている年代やらよく売れる時間帯を調べなくてはいけないといった感じで。
社会に出たら数学なんていらないでしょといって数学をないがしろにする人がいますが、意外と仕事で必要になってくるのですよ。
その時数学が得意だとスムーズに仕事ができますよね。
なので、私は文系の方にも数学を勉強していただきたいです。
得になることはあっても、損することはないです。
実は、理科、社会、数学は一つの物事を無理やり分類しただけなので、切っても切れない関係にあるのです。
例えば、社会の勉強なのに時差を求める問題で計算をしなきゃいけない。
また、理科の地震の単元では地震の伝わる速さを求めないといけない。
そんな感じでつながっているのです。
切り離せるのは言語の教科くらいです。
少し脱線しましたが、色んなことをピンポイントではなく大きくとらえると理解しやすくなります。
なので、私は数学苦手だからと決めつけないで少しずつ理解していくと分かるようになってきます。
その努力をするかしないかはあなた次第です!
スポンサーリンク









